Título: Bifurcações de Codimensão 2 para Campos Vetoriais Reversíveis
Autores: SOUZA, S.A; MEDRADO, J.C.R.
Instituto de
Matemática e Estatística
Endereço
eletrônico: Aluna: Sigreice Ariomar de
Souza
sigreiceariomar@yahho.com.br
Orientador: João Carlos da Rocha Medrado
joaocarlosmedrado@yahoo.com.br
Palavras chave:
Formas Normais, Bifurcações, Campos Vetoriais Reversíveis
Introdução:
Consideremos um campo
vetorial reversível de dimensão quatro, tendo um ponto fixo na origem, e tal
que 0 é um autovalor de multiplicidade quatro da parte linear de um bloco de
jordan 4 x 4. Esta é a singularidade de codimensão 2 para campos vetoriais
reversíveis.
O objetivo deste
trabalho é estudar a dinâmica de tais campos vetoriais. Obteremos a forma
normal para o campo vetorial , faremos o estudo local próximo dos pontos fixos e o cálculo das formas normais próximo
às curvas.
Material e Método ( Metodologia)
·
Uso de acervo
bibliográfico (periódicos);
·
Intercâmbio com
outros centros de pesquisa;
·
Realização de
seminários e/ou estudo dirigido com participação dos professores do IME – UFG e
de outros centros de pesquisa;
·
Uso de softwares
maremáticos, principalmente o maple, para efetuar cálculos e esboço de planos
de fase de campos vetoriais.
Resultados e Discussão
Consideremos um campo vetorial em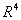 
da seguinte forma:
= L
X + R(X)
onde L
é um operador linear dado pela seguinte matriz:
L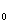
= 
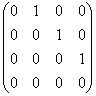
e R é uma função não
linear regular.
Temos que 
= L
X + R(X) é reversível, isto é, Dj(X) = - X(j), onde j é a involução.
Observando que: j
= Id, j L
= - L
j, j R(X) = - R(j X).
Em particular, seja j =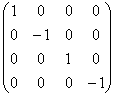 
Dado um grau p,
podemos encontrar um polinômio pela troca de variáveis tal que, para uma ordem p, a função R é
representada pela função N satisfazendo a seguinte equação diferencial parcial
linear:
DN(X) L
= L
N(X)
que é equivalente a
dizer que N comuta com o grupo gerado pela transposta L
de L
. Conservamos a propriedade que j N = - N j do problema
original. Denotamos por x
e N
, j = 1, 2, 3, 4 as componentes de X e N em 
. Temos que:
N
(jX) = (-1)
N
(X)
¶
N
= 0, ¶
N
= N
, para j = 2, 3,4
onde o operador ¶
é definido de alguma função regular f próximo de 0 por:
¶
f = Df(X) L
X = x
+ x
+ x
Abaixo se encontram
algumas soluções f para ¶
f = 0. As seguintes são integrais primeiras de graus 1, 2, 3,
4 respectivamente:
p
= x
p
= x
- 2x
x
p
= x
- 3x
x
x
+ 3x
x
p
= 3 x
x
- 6 x
x
- 8x
x
+ 18x
x
x
x
- 9x
x
Utilizaremos o seguinte
resultado: “ Alguma solução polinomial de ¶
f = 0 é um polinômio P de variáveis p
, p
, p
, p
. Como consequência , pode ser escrito como: P
( p
, p
, p
) + p
P
( p
, p
, p
), onde P
e P
são ambos polinômios de seus três argumentos”.
Pelo resultado acima,
e observando que o operador reversibilidade j leva invariante p
, p
, p
, muda p
para - p
e de N
(jX) = (-1)
N
(X), temos que:
N
(X) = p
P
( p
, p
, p
)
Introduzimos
agora os seguintes novos polinômios q
, r
, s
definidos por:
¶
q
= p
, ¶
r
= q
para j = 1, 2, 3
e ¶
s
= r
para j = 1, 3
Obtemos em seguida:
N
= q
P
( p
, p
, p
) + p
P
( p
, p
, p
) + p
Q ( p
, p
) + R(p
)
N
= r
P
( p
, p
, p
) + q
P
( p
, p
, p
) + q
Q ( p
, p
) + p
P
( p
, p
, p
)
N
= s
P
( p
, p
, p
) + r
P
( p
, p
, p
) + r
Q ( p
, p
) + q
P
( p
, p
, p
) + P
( p
, p
, p
).
Portanto a forma
normal para o campo vetorial é dada
por:
= L
X + P
( x
, p
, p
)
+ P
( x
, p
, p
) 
+ Q ( p
, p
) 
+
+ P
( x
, p
, p
)
+ P
( x
, p
, p
)
Em seguida faremos o
estudo local próximo dos pontos fixos da forma normal, a matriz da derivada
nesses pontos fixos, e a partir disso estudaremos a posição dos quatro autovalores no plano complexo.
Conclusões
É válido salientar que apenas pequena parte da dissertação foi apresentada neste resumo e resultados posteriores de maior importância serão apresentados no decorrer do desenvolvimento da tese.
Com base na teoria
vista, pretendo ampliar meus conhecimentos sobre campos vetoriais reversíveis
e formas normais, contribuindo para o
progresso da matemática.
Referências Bibliográficas
Belitskii, G. [1981] Normal forms relative to a filtering action
of a group, Trans. Mosc. Math. Soc., 40, 1- 39.
Elphick, C.,
Tirapegui, E., Brachet, M., Coullet, P. and Iooss, G. [1987] A simple global characterization for normal forms of singular vector
fields, Physica D, 29, 95 – 127.
Ioos,
G.,Kirchgassner, K. [1992] Water waves
for small surface tension: An approach via normal form, Proc. Roy. Soc.,
Edinburgh A, 122A, 267-299.
Iooss, G. and
Péroueme, M.C. [1993] Pertubed homoclinic
solutions in reversible 1:1 resonance vector fields, J. Diff. Eq.,102, 1,
62-88.