ANÁLISE NUMÉRICA DAS VIBRAÇOES DE CASCAS TOROIDAIS
SOARES, R.
M;
renatajl@cultura.com.br
ALMEIDA,
S. R. M.;
DEL
PRADO, Z. J. G. N.
Curso de
Mestrado em Engenharia Civil, Escola de Engenharia Civil - EEC-UFG.
Palavras chave: Cascas toroidais, vibrações livres.
1. INTRODUÇÃO
Cascas toroidais e cascas cilíndricas são elementos
estruturais amplamente utilizados em diversas áreas da engenharia tais como
mecânica, naval, off-shore, nuclear, etc. Assim, o comportamento destas cascas
tem sido estudado usando-se uma variedade de métodos numéricos e um aspecto
importante no projeto destas estruturas, é a determinação de suas freqüências
naturais, modos de vibração e respostas no tempo. O comportamento dessas cascas
tem sido estudado por diversos pesquisadores, usando métodos baseados em
teorias lineares para cascas finas, tais como Leung e Kwok (1994), Bert et al (1996) e Ming et al
(2002).
2.
OBJETIVOS
Como objetivo geral deste trabalho, têm-se os estudos
do comportamento das vibrações livres e forçadas de cascas toroidais,
realizando uma análise paramétrica das cascas, variando as condições de contorno
e os comprimentos na direção meridional da casca. Além disso, realizar uma comparação entre os
diversos métodos utilizados na análise de vibrações e estudar a resposta no
tempo da estrutura. A solução do
problema é desenvolvida através das teorias lineares de cascas de DMV e
Sanders. São apresentados as freqüências naturais e os respectivos modos de
vibração para cascas incompletas com diversas geometrias, calculados através do
método analítico e do Método da Quadratura Diferencial (DQM) Os resultados numéricos
calculados são validados pela comparação com resultados obtidos da solução pelo
Método de Elementos Finitos (FEM).
3.
METODOLOGIA
Considera-se uma casca toroidal elástica, homogênea e
isotrópica, com módulo de elasticidade E e coeficiente de Poisson n. A geometria da casca é descrita por um raio
meridional R, por um raio r da sua seção transversal circular, espessura h (com
h << R), e ângulo interno total f. As coordenadas meridional, circunferencial e radial
são, respectivamente, h, q e W
e os deslocamentos correspondentes são u, v e w como se mostra na Figura (1).
Usando as teorias de cascas Donnell-Mushtari-Vlasov (DMV) e
Sanders, partindo do funcional de energia da casca, com o uso do cálculo
variacional obtêm-se as equações diferenciais da casca. Escrevendo as equações
de equilíbrio em função das resultantes dos esforços internos temos o sistema
de equações com base na teoria linear DMV:
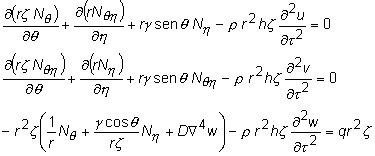 (1)
(1)
onde t é a coordenada temporal e Ñ é o operador de Laplace.
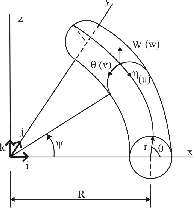
Figura 1
- Geometria da casca e sistema de coordenadas
Para resolver o sistema de equações diferenciais, utilizamos o
método de Galerkin aproximando o campo de deslocamento por séries de Fourier
nas direções circunferencial e meridional. Reduz-se o problema de estabilidade
em um problema de autovalor e da sua solução, obtêm-se o parâmetro crítico e o
modo crítico. Na análise através do DQM, o domínio é dividido em uma malha de
pontos e, em cada ponto, de uma determinada direção, um somatório de
coeficientes de peso substitui os diferenciais. Os coeficientes de peso são
determinados pela função de teste. Aplicando as regras da quadratura para as
derivadas, encontram-se as equações na forma do método da quadratura
diferencial (Bert e Malik, 1996). A união do domínio com as equações de
contorno produz um sistema de equações lineares, onde estão associadas as
condições de contorno e as equações da quadratura diferencial. Novamente,
tem-se um problema de autovalor que fornece as freqüências naturais e os
respectivos modos de vibração.
4. RESULTADOS
NUMÉRICOS
Foi adotada uma casca com: h = 0,01 m; r = 1 m; R = 2,5465 m; E = 2,07 x 108 kN/m2;
n = 0,3; r = 7800 kg/m3.
Foram analisadas as vibrações livres de cascas
toroidais e cilíndricas, engastadas e apoiadas em ambas extremidades. As cascas
toroidais foram analisadas com comprimentos meridionais (Ry) variados.
O
programa comercial ANSYS foi usado para validar os resultados obtidos através
do método da quadratura diferencial e do método analítico. Nas modelagens por
elementos finitos e através do método da quadratura diferencial, foram
utilizadas diversas malhas dependendo do valor do ângulo y. Nas Figuras 2 e 3 são apresentados os diversos
resultados encontrados na análise.
|
(a) |
(b) |
(c) |
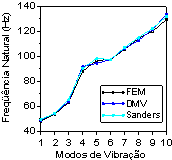
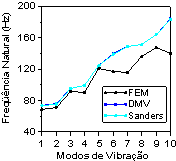
Figura 2 –
Freqüências da casca cilíndrica (a) Apoiada (b) Engastada. (c) 1ºModo de
vibração
|
(a) |
(b) |
|
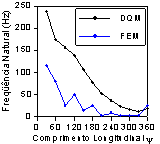
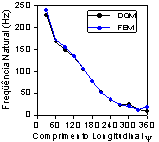
Figura 3
Freqüências da casca Toroidal (a) Apoiada (b) Engastada. (c) 1ºModo de vibração
da casca biapoiada com y = 900º
4. CONCLUSÕES
Observou-se que a teoria DMV apresenta boa precisão de resultados quando
comparada com a teoria de Sanders. Os
resultados encontrados pelo método da quadratura diferencial, validados através
do uso do programa de elementos finitos ANSYS, mostram excelente convergência
para o caso de condições de contorno engastada; enquanto que para cascas apoiadas sua precisão é
muito grosseira. O método da quadratura
diferencial é ferramenta na análise de cascas de geometria complexa com
condições de contorno engastada, sendo limitado na aplicação para alguns tipos especiais de condições
de contorno em problemas multidimensionais.
REFERÊNCIAS BIBLIOGRÁFICAS
BERT, C. W. e MALIK, M., , Differential quadrature method in
computational mechanics: A review. ASME
Applied Mechanics Review, vol. 49, pp. 01-27. 1996
LEUNG, A Y. T. e
KWOK, N. T. C., Free vibration of a toroidal Shell. Thin-walled structures, vol. 18, pp.317-332, 1994
MING, R.S.; PAN,
J.; NORTON, M.P., Free vibrations of elastic circular toroidal shells. Applied acoustics, vol. 63, pp.
513-528, 2002.
NOVOZHILOV,
V. V., Thin shell theory. 2. ed. Groningen: P. Noordhoff Ltda,
1964
ZHANG, F.;
MIRFAKHRAEI, P.; XU, B.; REDEKOP, D., A computer program for the elastostatics
of a toroidal shell using the differential quadrature method. International Journal of Pressure Vessels
and Piping, vol. 75, pp. 919-929, 1998.
Agradecimentos
Esta pesquisa foi desenvolvida graças
ao apoio do CNPq através da concessão de uma bolsa de mestrado.