Neste trabalho, introduzimos e investigamos estatisticamente um novo estado de campo eletromagnético, chamado de Estado de Número Deslocado Não Linear (ENDNL), definido como:
.
Tal estado é obtido através da aplicação de um meio não linear, representado pela função 
, no Estado de Número Deslocado Linear (ENDL). Observe que para 
, obtemos o ENDL como caso particular.
Este meio é provido de propriedades que entre outras, contribui para uma vibração especial para a freqüência de oscilação do campo eletromagnético, que depende da energia. A influência da fase e suas várias propriedades não clássicas foram estudadas de forma comparativa e discutidas, ao aplicarmos os efeitos da não linearidade no Estados de Número Deslocado.
Definimos o ENDNL e obtivemos os seus coeficientes da representação de número, dados por:
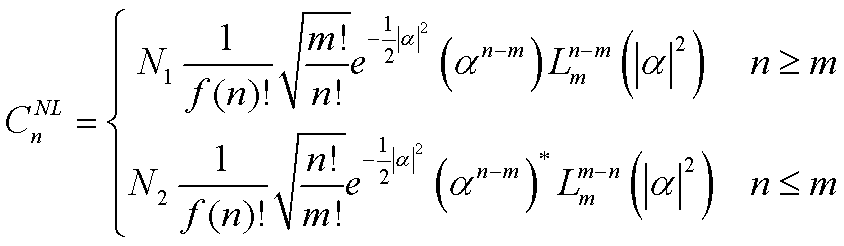
Baseado na forma como definimos, pudemos então levantar uma proposta para a geração deste estado, que contém como casos particulares alguns estados já investigados na literatura, como por exemplo, o estado de número e o Estado Coerente Não Linear.
As propriedades estatísticas de um estado qualquer podem ser investigadas sempre que tenhamos os seus coeficientes. Neste sentido investigamos para o ENDNL a sua Função Distribuição de Número de Fótons (P(m)) e a Função de Probabilidade no Espaço de Fase Q(b) de Husime.
O estudo das propriedades estatísticas para este estado, em principal a Função Distribuição de Número de Fótons e a Função de Probabilidade no Espaço de Fase Q(b) de Husine, revelou-nos que ele, apresenta efeito de redução nos picos da Distribuição de Número de Fótons (conforme Fig. 01), efeito de redução do ruído quântico apresentando em particular compressão de número e fase (conforme Fig. 02), o que nos surpreende pois este efeito não está presente no Estado de Número Deslocado Linear, tais fatos demonstram que o estado proposto é relevante e portanto deve ser incluído na literatura.
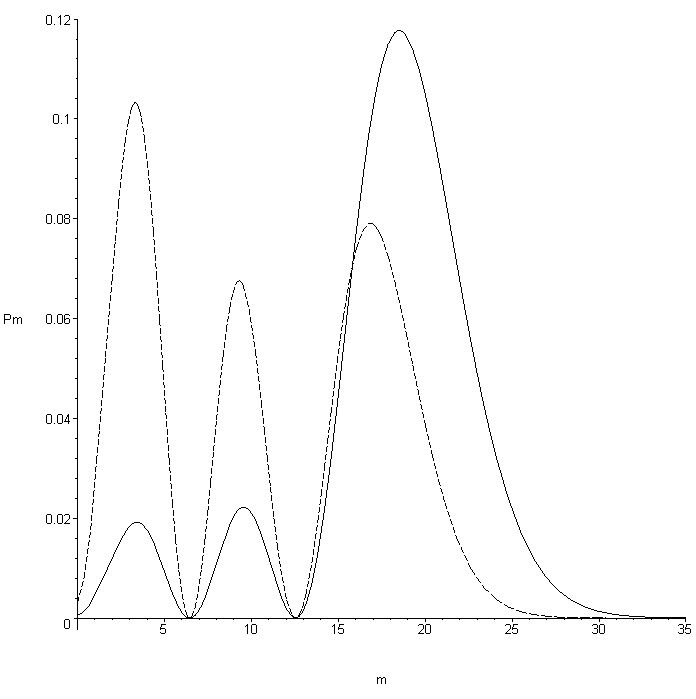
Figura 01 – Distribuição de Número de Fótons para o ENDNL com número inicial de fótons n = 2, parâmetro de deslocamento a = 3 e coeficiente de não linearidade k=0,007. Para comparação mostramos o END (linha pontilhada) correspondendo a k=0.
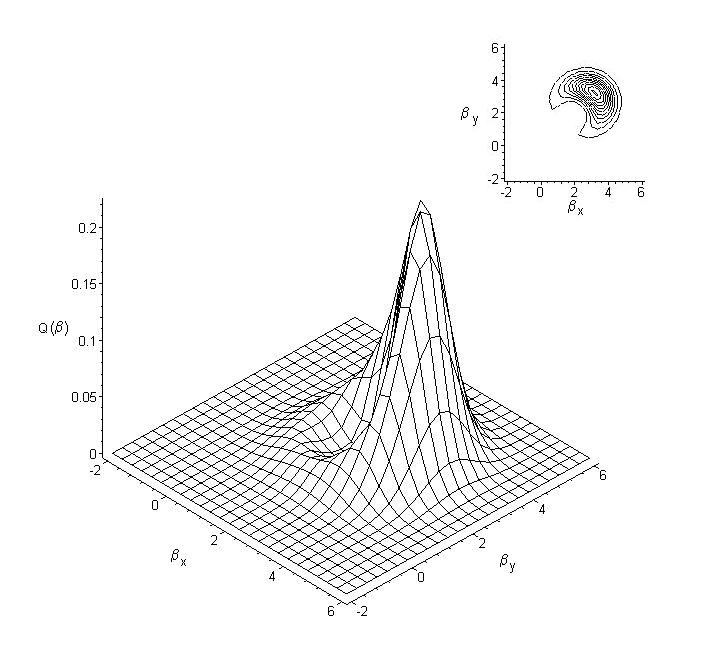
Figura 02 – Função de Husime Q(b) para o ENDNL com número inicial de fótons n = 2, parâmetro de deslocamento a = 3eip/4 e coeficiente de não linearidade k=0,007. Para comparação mostramos a respectiva curva de nível.
Neste trabalho definimos o Estado de Número Deslocado Não Linear, que é obtido pela passagem do Estado de Número Deslocado através de um meio não linear. O efeito da não linearidade foi investigado e mostra que novo estado do campo eletromagnético possui efeitos quânticos de compressão, chamada de compressão de número-fase nas variáveis, e é devida as altas ordens de não linearidade do meio. Mostramos este efeito através da curva de nível da Função de Husime, quando estas possuem a forma curvada representa compressão de número-fase, ao contrário da compressão de quadratura em que as curvas de níveis são do tipo elípticas.
Este efeito é de grande importância no domínio da Óptica Quântica, uma vez que representa uma boa aproximação para o Estado de Número de Fótons, que é de difícil obtenção em laboratórios nos dias atuais.
[1] F.A.M. Oliveira, M.S. Kim, P.L. Knight and V. Buzek. Phys. Rev. A41, 2645(1990).
[2] R.J. Glauber. Phys. Rev. 131, 2766 (1963).
[3] S. Sivakumar. Phys.Lett. A250, 257 (1998).
[4] Stefano Mancini. Phys. Lett. A233, 291(1997).
[5] V.I. Man’ko, G. Marmo, E.C.G. Sudarshan and F. Zaccaria. Phys. Scrip. 55, 528 (1997).