Com o atual avanço na tecnologia de preparação e crescimento de materiais semicondutores e a manipulação de feixes de laser é possível atualmente aprisionar um número finito de elétrons ou íons em regiões pequenas. Essas armadilhas são criadas pela imposição de um potencial de confinamento artificial. Como exemplo temos: elétrons confinados em bolhas e "covas" sobre a superfície do hélio líquido, armadilhas a laser e de rádio-frequências para íons, elétrons em plasma [1] e elétrons em ponto quântico em estruturas semicondutoras [2]. Elétrons sobre hélio líquido e íons confinados em armadilhas obedecem a mecânica clássica devido a baixas densidades e pela grande massa dos íons respectivamente.

Neste trabalho aplicamos a Dinâmica Molecular (DM) para estudar algumas propriedades físicas deste sistema clássico bidimensional contendo um número finito de elétrons interagentes e confinados por um potencial externo (mais detalhe: veja seção dos objetivos). Os resultados apresentados estão baseados na hipótese de que a dinâmica clássica, considerando a interação de dois corpos, descreve muito bem a dinâmica dos elétrons na maioria dos sistemas citados acima.

De uma maneira geral a dinâmica molecular é um método de simulação que permite a partir de equações clássicas de movimento descrever o comportamento microscópico de um sistema de muitos corpos. A essência do método e a equação de Newton, com isso a questão fundamental do método é conhecer o potencial de interação entre as partículas do sistema. Com o conhecimento do potencial de interação, as equações de movimento são integradas usando o Algoritmo predictor-corrector de Gear. A partir da evolução do sistema em equilíbrio termodinâmico as médias estatísticas de propriedade de interesse são realizadas permitindo o conhecimento por exemplo da estrutura em nível atômico, a dinâmica dos átomos e as propriedades termodinâmicas.

Neste trabalho reproduzimos inicialmente os resultados conhecidos da literatura para ter certeza que nosso código funcionava corretamente. Em seguida estudamos um sistema com k=0 e α=1, onde calculamos a energia do estado fundamental para vαrios aglomerados e analisamos suas estruturas. Investigamos o efeito de temperatura na transição ordem-desordem através do monitoramento das trajetórias das partículas durante a evolução do sistema em equilíbrio termodinâmico, em seguida estudamos os efeitos de anisotropia e finalmente o efeito de blindagem nas propriedades estruturais e termodinâmicas para vários tamanhos de aglomerados.

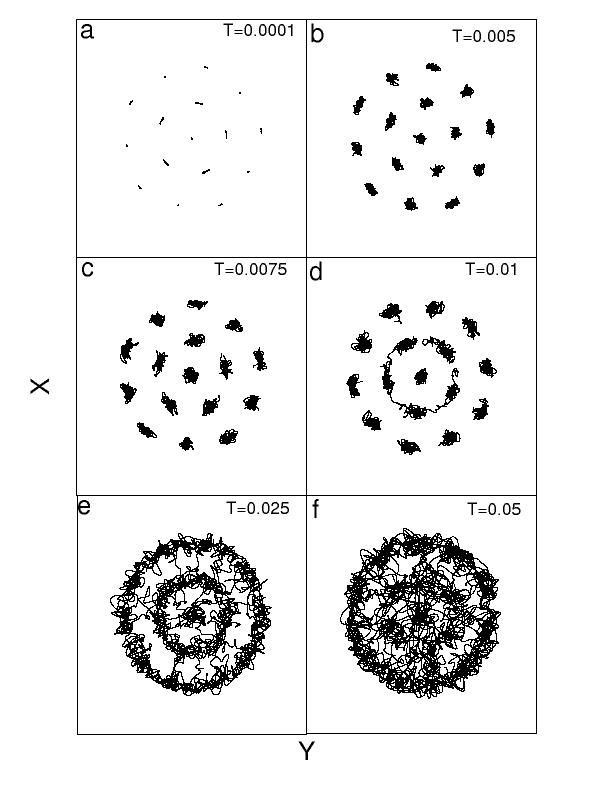
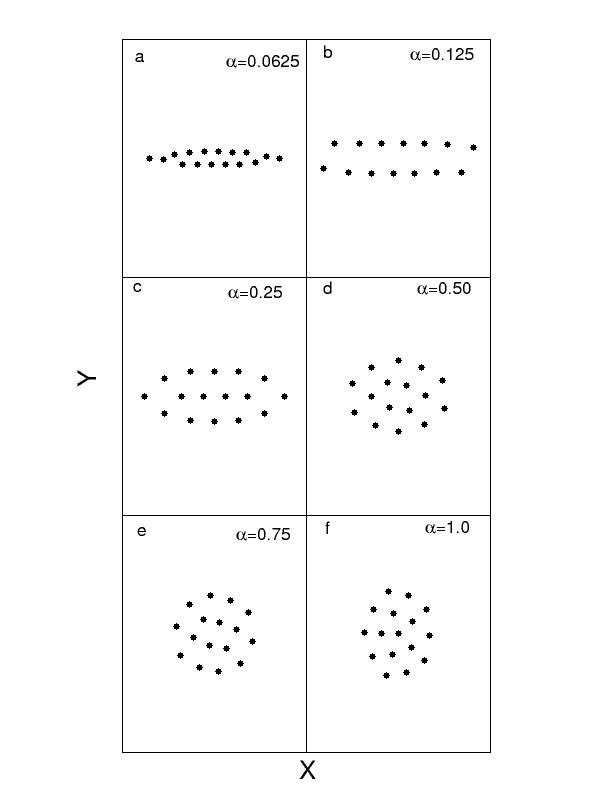
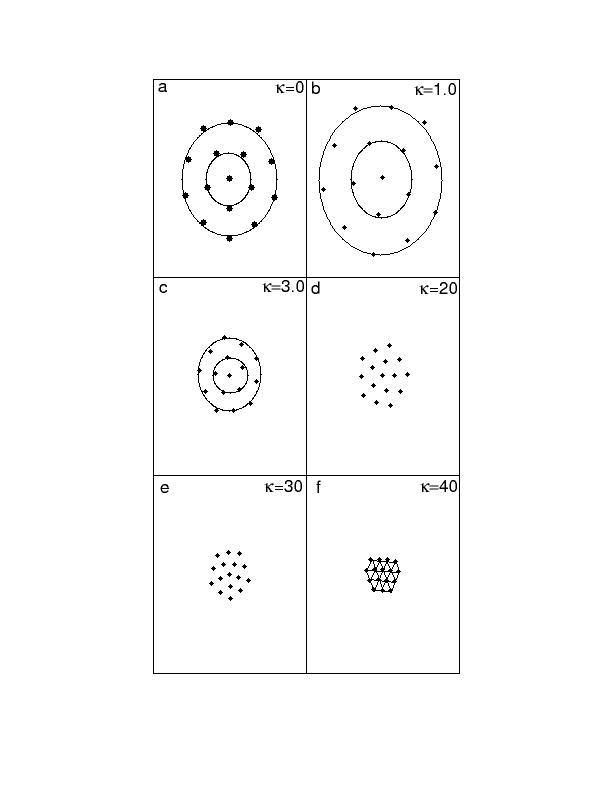
As figuras 1, 2 e 3 apresentam resultados de simulação de dinâmica molecular para um aglomerado de 16 partículas. A figura 1 mostra a transição de fase ordem-desordem para o sistema aquecido lentamente, observamos a difusão angular para temperatura variando de T=0.0075 a 0.01 e difusão radial acontecendo entre T=0.01 a 0.025. Em seguida na figura 2 temos a configuração do estado fundamental do sistema para valores decrescentes do parâmetro de anisotropia α, verificamos que o sistema apresenta várias transições indo desde um sistema bidimensional até atingir uma configuração unidimensional do tipo zig-zag. Finalmente na figura 3 mostramos o efeito da blindagem sobre as configurações do estado fundamental do sistema, o qual muda sua estrutura com valores crescentes de k , saindo da estrutura de camadas na forma circular até atingir a rede de Wigner.

Figura 1 Figura 2 Figura 3

Usando a DM realizamos várias simulações para um sistema bidimensional com interação Coulombiana e confinado parabolicamente, isto é, com κ=0, para vários tamanhos de aglomerados de cargas onde calculamos o valor da energia e as configurações do estado fundamental. Reproduzimos alguns resultados da literatura que tinham sido obtidos através do método de Monte Carlo. Observamos que para sistemas pequenos os elétrons se organizam em uma estrutura de anéis e que para sistemas maiores a estrutura mais estável é uma rede triangular conhecida como rede de Wigner, essas configurações são consequências da competição entre a interação elétron-elétron e o potencial confinante (parabólico).

Realizamos também um estudo do efeito de temperatura para um aglomerado de 16 partículas, observamos que este sistema apresenta duas temperaturas críticas para as transições ordem-desordem em intervalos distintos. Inicialmente temos a difusão radial no intervalo de temperatura T=0.0075 a 0.01, e aquecendo um pouco mais o sistema temos mais uma difusão angular, que acontece no intervalo de temperatura T=0.01 a 0.025.

O passo seguinte foi o estudo do efeito do parâmetro anisotrópico no valor da energia por partícula. A medida que o parâmetro α diminui, a estrutura do sistema se modifica, tornando-se uma estrutura elíptica, e que os elétrons das camadas mais interna tende a pular para a camada mais externa até chegar no limite em que a estrutura se aproxima de uma estrutura unidimensional. Podemos concluir também que a energia por partícula é uma função razoavelmente suave com α, mas nenhum efeito na energia devidos as transições estruturais ocorridas são visíveis.

Finalmente estudamos o efeito do parâmetro de blindagem nas propriedades estruturais e termodinâmicas deste sistema. Onde verificamos que a ocupação das camadas muda consideravelmente como função do parâmetro de blindagem, e para grandes blindagens, (k=0), a estrutura de camadas desaparece e as partículas formam uma rede de Wigner. Com isso atingimos os objetivos propostos para este projeto.

[1]Bolton, F. e Rossler, U. Superlatt. Microstruct. Vol. 13, pág. 139 (1993).

[2]Benadov, V. M. e Peeters, F. M. Phys.Rev. B, Vol. 49, pág. 2667 (1994).

Os autores agradecem ao Conselho Nacional de Desenvolvimento Científico - (CNPq) pelo suporte financeiro.