ESTUDO DA VARIABILIDADE DOS INTERVALOS ENTRE DISPAROS EM MODELOS DE MOTONEURÔNIOS COM DENDRITO PASSIVO
Vieira, M.F. e Kohn, A.F.
Faculdade de Educação Física – UFG – marcus@fef.ufg.br
Palavras Chave – Motoneurônio, Modelagem Matemática, Simulação de Sistemas Biológicos
1 Introdução
Quando um motoneurônio dispara com uma freqüência média constante a informa-ção provavelmente é transmitida na seqüência de intervalos entre os disparos (cujo in-verso fornece a freqüência instantânea) que, entretanto, são variáveis. A operação do sistema nervoso em geral é marcada por uma variabilidade que dificulta a análise de qualquer atividade neuronal. Entretanto, tal variabilidade é um mecanismo funcional muito importante. Ela pode ser fundamental ao estabelecer uma relação precisa entre as propriedades de disparo de um receptor e o estímulo, enquanto que a saída variável e ruidosa de um motoneurônio pode contribuir na obtenção de uma resposta mecânica mais suave (ao diminuir o sincronismo entre os motoneurônios, por exemplo) [1,2].
Esta variabilidade é principalmente causada por flutuações nas entradas sinápti-cas, isto é, o motoneurônio deve integrar um grande número de potenciais pós-sináp-ticos no tempo e no espaço em seus diversos sítios sinápticos. Tal variabilidade, ineren-te a este processo de somação temporal e espacial, é denominada de ruído sináptico.
2 Metodologia
As simulações foram realizadas com os modelos de motoneurônios desenvolvidos pelos autores, cuja descrição detalhada pode ser encontrada em outros trabalhos [3,4,5,6,7].
Ao invés de modelar o decurso temporal das condutâncias sinápticas por uma função alfa, é mais conveniente para fins de simulação computacional obter uma descrição por uma equação diferencial de segunda ordem:![]() (1).
(1).
e seu pico máximo e o instante no qual este pico máximo ocorre são dados por:
![]() (2) e
(2) e ![]() (3).
(3).
A equação diferencial de segunda ordem mostrada em 1 pode ser descrita por um sistema de equações diferenciais de primeira ordem do tipo:
![]() (4) e
(4) e ![]() (5), na qual c
(t) é uma função impulso que dispara a condutância sináptica.
(5), na qual c
(t) é uma função impulso que dispara a condutância sináptica.
A corrente sináptica será descrita por ![]() (6), na qual Isin é a corrente sináptica em um dado segmento dendrítico; Gmax é a condutância sináptica máxima deste segmento dendrítico igual à condutância de uma única sinapse vezes o número de sinapses existentes neste segmento dendrítico; Gsin fornece o curso temporal da condutância sináptica segundo a equação 5; Esin é o potencial de equilíbrio sináptico e Vm é o potencial de membrana deste segmento dendrítico.
(6), na qual Isin é a corrente sináptica em um dado segmento dendrítico; Gmax é a condutância sináptica máxima deste segmento dendrítico igual à condutância de uma única sinapse vezes o número de sinapses existentes neste segmento dendrítico; Gsin fornece o curso temporal da condutância sináptica segundo a equação 5; Esin é o potencial de equilíbrio sináptico e Vm é o potencial de membrana deste segmento dendrítico.
Dividimos a condutância sináptica Gsin por seu máximo ![]() (semelhante à equação 2 com a
¹
1,0) a fim de normalizá-la em um valor igual a 1,0, de forma que ao multiplicarmos pela condutância sináptica máxima Gmax do respectivo segmento dendrítico obteremos a condutância sináptica com o valor e o curso temporal desejado e próprio daquele segmento dendrítico. Com esta modelagem obtém-se a somação da condutância sináptica bem como, pela escolha de uma função c
(t) adequada, pode-se obter as ativações repetitivas desejadas. Como função de entrada c
(t) escolhemos um processo Poisson que produz os disparos repetitivos na condutância sináptica e com a aleatoriedade própria das entradas sinápticas no motoneurônio.
(semelhante à equação 2 com a
¹
1,0) a fim de normalizá-la em um valor igual a 1,0, de forma que ao multiplicarmos pela condutância sináptica máxima Gmax do respectivo segmento dendrítico obteremos a condutância sináptica com o valor e o curso temporal desejado e próprio daquele segmento dendrítico. Com esta modelagem obtém-se a somação da condutância sináptica bem como, pela escolha de uma função c
(t) adequada, pode-se obter as ativações repetitivas desejadas. Como função de entrada c
(t) escolhemos um processo Poisson que produz os disparos repetitivos na condutância sináptica e com a aleatoriedade própria das entradas sinápticas no motoneurônio.
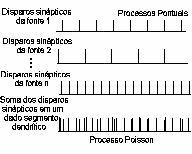 Figura 1 – Os disparos sinápticos em um dado segmento dendrítico do motoneurônio podem ser descritos por um processo Poisson, que consiste na soma (ou superposição) dos disparos sinápticos de cada uma das fontes que chegam ao motoneurônio, cada um deles descrito por um processo pontual.
Figura 1 – Os disparos sinápticos em um dado segmento dendrítico do motoneurônio podem ser descritos por um processo Poisson, que consiste na soma (ou superposição) dos disparos sinápticos de cada uma das fontes que chegam ao motoneurônio, cada um deles descrito por um processo pontual.
3 Resultados
A análise da variabilidade dos intervalos entre disparos por meio de simulações foi realizada, sobretudo, com o motoneurônio tipo S, uma vez que os dados levantados experimentalmente (tabela 1, figura 2-Esq.) e aqueles mais adequados reportados na literatura dizem respeito a disparos de unidades motores dos músculos sóleo e gastrocnêmio em condições de contrações fracas, constituídos portanto quase que na totalidade por unidades motoras de contração lenta do tipo S. Alguns dados obtidos por meio de simulações estão mostrados na tabelas 2 e figura 2 (Dir.), cujo título descrevem quais sinapses estavam ativas e sua distribuição.
Tabela 1
Estatística dos Dados Obtidos Experimentalmente*
|
Aquisição |
Músculo |
Perna |
Posição |
No de Intervalos |
Freqüência Média (imp/s) |
Coef. De Variação |
Assimetria |
Dispersão |
|
1 |
Sóleo |
esquerda |
sentado |
618 |
7,6604 |
0,1055 |
4,4823 |
43,0382 |
|
2 |
Sóleo |
esquerda |
em pé |
613 |
7,4523 |
0,1393 |
0,8389 |
9,4249 |
|
3 |
Sóleo |
esquerda |
sentado |
614 |
7,4160 |
0,1606 |
0,9616 |
6,9957 |
Conclusão
Pelas simulações observamos que o coeficiente de variação aumenta com a diminuição da freqüência média de disparo do motoneurônio, dado amplamente reportado na literatura; em todas as situações de simulação, o coeficiente de variação diminuiu notavelmente quando aumentamos a resistência de entrada do motoneurônio; nas simulações nas quais a resistência de entrada do motoneurônio foi aumentada, o coeficiente de variação aproxima-se de valores obtidos experimentalmente; as simulações nas quais as sinapses foram distribuídas uniformemente ao longo do dendrito equivalente apresentam menor coeficiente de variação; as simulações nas quais as sinapses localizam-se longe do soma apresentam menor coeficiente de variação, e este é tanto menor quanto maior a distância das sinapses ao soma; os histogramas apresentam-se perfeitamente compatíveis com aqueles reportados na literatura sendo assimétricos, positivamente desviados; os histogramas são cada vez mais assimétricos, positivamente desviados à medida que decresce a freqüência média de disparo do motoneurônio.
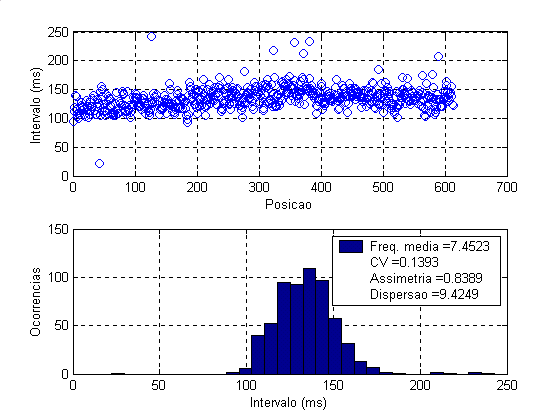
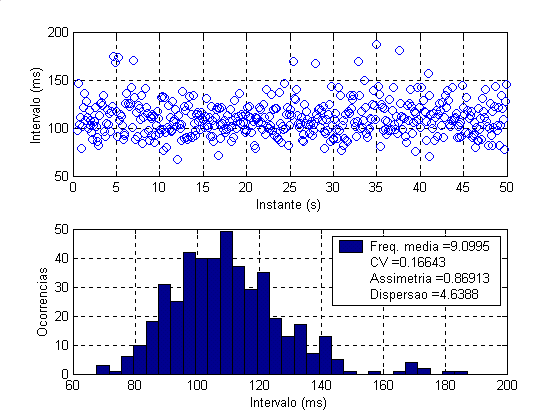
Figura 2 – Esq.-Gráfico e histogramas dos intervalos entre disparos da aquisição número 2 da tabela 1. Dir.- Idem da simulação número 2 da tabela 2.
Tabela 2
Simulações Somente com Sinapses Excitatórias Distribuídas como Ia a partir do Dendrito Zero-Motoneurônio Tipo S
|
Simulação |
No de Intervalos |
Freqüência Média (imp/s) |
Coef. De Variação |
Assimetria |
Dispersão |
|
1 |
453 |
9,1337 |
0,1598 |
0,8492 |
4,0525 |
|
2 |
451 |
9,0995 |
0,1664 |
0,8691 |
4,6388 |
|
3 |
454 |
9,1531 |
0,1779 |
0,8908 |
4,1014 |
Referências
[1] POLIAKOV, A.V.; MILES, T.S.; NORDSTROM, M.A. Discharge patterns of tonically firing human motoneurones. Biological Cybernetics, v.73, p.189-194, 1995.
[2] WARREN, J.D.; MILES, T.S.; TÜRKER, K.S. Properties of synaptics noise in tonically active human motoneurons. Journal of Electromyography na Kinesiology, v.2, n.4, p.189-202, 1993.
[3] Vieira, M.F. Novos Modelos de Motoneurônios de Vertebrados. São Paulo, SP:USP, 2002. Tese de Doutorado, Universidade de São Paulo, 2002. 304 p.
[4] Vieira, M.F.; Kohn, A.F. Novos Modelos de Motoneurônios de Vertebrados. In: XVIII Congresso Brasileiro de Engenharia Biomédica, 2002, São José dos Campos – SP. Anais do XVIII Congresso Brasileiro de Engenharia Biomédica, São José dos Campos - SP, 2002. 1 CD-ROM.
[5] Vieira, M.F.; Kohn, A.F. The encoding of input currents by motoneurons in relation to neuronal modelling. In: IV Neuronal Coding Workshop, 2001, Plymouth. Annals of IV Neuronal Coding Workshop, Plymouth, 2001a, p.6-9.
[6] Vieira, M.F.; Kohn, A.F. Uma nova proposta para modelos de motoneurônios de diferentes tamanhos. In: V Congresso Brasileiro de Redes Neurais, 2001, Rio de Janeiro. Anais do V Congresso Brasileiro de Redes Neurais, Rio de Janeiro, 2001b, p.127-132.
[7] Kohn, A.F.; Vieira, M.F. Optimality in the encoding/decoding relations of motoneurones and muscle units. BioSystems, v. 67, p. 113-119, 2002.