MODELOS DE MOTONEURÔNIOS TIPOS S, FR E FF

1 Universidade Federal de Goiás-Faculdade de Educação Física-Goiânia-GO

2 Universidade de São Paulo-Escola Politécnica-São Paulo-SP

Palavras Chave: Modelos de Motoneurônios, Validação de Modelos Neuronais, Modelos Neuronais Biofísicos

O motoneurônio é o elemento de interface entre o sistema nervoso e as fibras musculares. Conhecer a "linguagem" por meio da qual o motoneurônio transforma os comandos de entrada originados no sistema nervoso central em comandos para os músculos é de capital importância para a ciência que estuda o controle motor, envolvendo o conhecimento das propriedades estáticas e dinâmicas do motoneurônio enquanto célula excitável. Relações e dados obtidos da análise do comportamento de modelos matemáticos fornecem importantes contribuições na elucidação desta "linguagem". Neste aspecto, o objetivo deste trabalho foi desenvolver três modelos matemáticos bastante fidedignos com a biologia de cada um dos três tipos de motoneurônio (S, FR e FF) encontrados em gatos, levando em conta tanto conhecimentos geométricos quanto biofísicos. Modelos publicados por outros pesquisadores serviram de ponto de partida para os novos modelos aqui apresentados [1,2,3,4,5]. Além disso, cada novo modelo deveria passar por uma bateria de testes biologicamente significativa, porque a maioria dos modelos de motoneurônios na literatura foi validada com um conjunto de testes relativamente restrito, a maioria dos quais com uma corrente de entrada constante.

Os modelos tipo S e FR derivaram, em parte, dos respectivos modelos desenvolvidos por Jones e Bawa [4,5], contendo, entretanto, algumas correntes iônicas completamente diferentes, o que permitiu melhorias substanciais na qualidade dos modelos. Adicionalmente, criamos um modelo para o motoneurônio tipo FF, completando assim o conjunto de motoneurônios modelados. A estrutura geral de cada modelo é mostrada na figura 1.

Para reproduzir as características do motoneurônio real, o modelo matemático do soma apresenta várias condutâncias iônicas voltagem-dependentes [6]. A equação diferencial geral do potencial de membrana é dada por:

(1)

na qual V_s é o potencial de membrana no soma, g_l,s é a condutância de fuga, E_l,s é o potencial de membrana de repouso, g_i são as condutâncias iônicas e E_i são seus respectivos potenciais de Nernst, g_s,do é a condutância de acoplamento entre o soma e o compartimento dendrítico d_o, V_do é o potencial de membrana do compartimento dendrítico d_o, g_s,is é a condutância de acoplamento entre o segmento inicial e o soma e V_is é o potencial de membrana do segmento inicial. Uma equação semelhante descreve o segmento inicial e os compartimentos dendríticos.

Dendrito Equivalente - A geometria do dendrito equivalente para os modelos tipo S e FR foi semelhante àquela adotada em Jones e Bawa [4,5], baseada em dados experimentais [7,8]. O dendrito equivalente possui 17 (19) compartimentos, cujo diâmetro diminui distalmente, com um comprimento eletrotônicos total de 7000 m m (6675 m m) no modelo tipo S (FR), ambos terminando em uma extremidade selada. Adotamos o modelo em degrau para os parâmetros dendríticos passivos [8]: resistividade específica da membrana 20000 W cm² (11000 W cm²) no dendrito e 700 W cm² (225 W cm²) no soma e segmento inicial para os modelos tipo S (FR). Em ambos os modelos a capacitância específica da membrana foi de 1,0 m F/ cm² e a resistividade citoplasmática específica de 70 W cm.

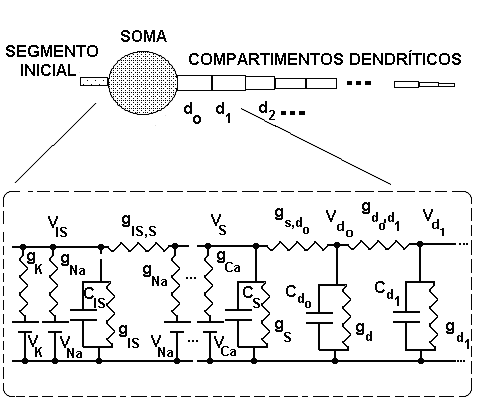
Figura 1 – Esquema geral dos modelos de motoneurônios. O soma e o segmento inicial são modelados pela associação em paralelo de uma capacitância e várias condutâncias voltagem-dependentes (apenas duas são mostradas no soma), cada uma delas em série com uma bateria.

Para modelar o dendrito equivalente do motoneurônio tipo FF usamos os resultados experimentais relativos à célula 41/2 [7.8]. O cabo equivalente resultou em um comprimento total de 6650 m m, representado por 19 compartimentos adjacentes: resistividade específica da membrana 20000 W cm² nos dendritos e 70 W cm² no soma e segmento inicial. A capacitância específica da membrana foi de 1,0 m F/ cm² e a resistividade específica citoplasmática de 70 W cm.

Segmento Inicial - O segmento inicial foi modelado como um cilindro selado com diâmetro de 10 m m e comprimento de 100 m m para os três modelos de motoneurônios. Os canais iônicos voltagem dependentes foram modelados como em Jones e Bawa [5,6] e Traub [1]: consistiram dos canais rápidos de Na⁺ e K⁺, semelhantes nos três modelos, com um limiar de disparo mais baixo do que o soma.

Soma - O soma foi modelado como uma esfera com um diâmetro de 50,9 m m no modelo do motoneurônio tipo S, 48,8 m m no do tipo FR e 49,2 m m no do tipo FF. Os canais rápidos de Na⁺ e K⁺ foram modelados como em Jones e Bawa [5,6], que foram adaptados do modelo de Traub [1]. As correntes lentas de K⁺ foram trocadas por duas outras correntes lentas de K⁺ que dependiam explicitamente da concentração intracelular de Ca⁺⁺: uma corrente do tipo SK e uma do tipo BK [9]. Dois tipos de corrente de Ca⁺⁺, tipo N e tipo L, contribuíram para as variações na concentração intracelular de Ca⁺⁺. Para o modelo de motoneurônio tipo FF, as principais considerações de modelos pré-existentes tiveram de ser cuidadosamente reformuladas para melhor representação do comportamento real do motoneurônio.

Este trabalho propôs novos modelos matemáticos de complexidade intermediária para os três tipos principais de motoneurônios de mamíferos. A validação dos novos modelos propostos incluiu comparações com o que é encontrado em biologia, desde simples valores de parâmetros até comportamentos estáticos e dinâmicos. O nível de complexidade do modelo é bastante adequado em investigações de muitos fenômenos de um único neurônio tais como interações dendríticas não lineares, propagação antidrômica de potenciais de ação na arborização dendrítica, variabilidade de trens de disparos devido a bombardeamentos sinápticos na arborização dendrítica e efeitos da sincronização de entradas sinápticas nas estatísticas dos trens de disparos do motoneurônio.

Acreditamos que os modelos também são adequados para uso em simuladores de redes de motoneurônios, se forem implementadas em máquinas razoavelmente rápidas com uma programação otimizada. Tais simuladores, para que sejam razoavelmente realísticos a nível neuronal, têm de incluir modelos de motoneurônios que tenham alguma representação das transformações espaço-temporais causadas pelos dendritos, além de incluir uma descrição do motoneurônio que possa dar conta das diferenças desde o tipo S ao tipo FF. A inclusão de dois tipos de canais de cálcio e dois tipos de canais lentos e cálcio-dependentes de potássio contribuíram para o comportamento biologicamente realístico dos modelos, tanto do ponto de vista biofísico quanto do ponto de vista de entrada/saída.

Relações biologicamente realísticas qualitativas/quantitativas encontradas nos três modelos incluem: a) resistência de entrada em ordem decrescente do modelo tipo S para o tipo FF; b) constante de tempo de membrana do soma em ordem crescente; c) reobase em ordem crescente; d) freqüência mínima de disparo para correntes de entrada constantes em ordem crescente e e) amplitude do pico e duração da AHP em ordem decrescente do modelo tipo S para o tipo FF.

[1]Traub, R. D. Motorneurons of Different Geometry and Size Principle. Biological Cybernetics, v.25, n.3, p.163-176, 1977.

[2]Traub, R. D. e R. Llinas. Spatial-Distribution of Ionic Conductances in Normal and Axotomized Motor-Neurons. Neuroscience, v.2, n.6, p.829-849, 1977.

[3]Booth, V., J. Rinzel e O. Kiehn (1997). Compartmental model of vertebrate motoneurons for Ca++ dependent spiking and plateau potentials under pharmacological treatment. Journal of Neurophysiology, v.78, p.3371-3385, 1997.

[4]Jones, K. E. e P. Bawa. Computer simulation of the responses of human motoneurons to composite 1A EPSPS: Effects of background firing rate. Journal of Neurophysiology, v.77, n.1, p.405-420, 1997.

[5]Jones, K. E. e P. Bawa. A comparison of human motoneuron data to simulated data using cat motoneuron models. Journal of Physiology-Paris, v.93, n.1-2, p.43-59, 1999.